RINGKASAN PERSAMAAN DIFERENSIAL BIASA.
I. PERSAMAAN DIFERENSIAL (PD) Orde Satu Derajat Satu.
1. PD yang bisa dipisah peubahnya dan Reduksi ke bentuk tersebut.
1.1. PD yang dapat dipisah peubahnya.
Bentuk Umum : M (x,y) dx + N (x,y) dy = 0 dengan M (x,y) dan N (x,y)
bisa difaktorkan atas faktor-faktor yang memuat x saja dan/atau y saja.

Sehingga :

Dan penyelesaian PD :

1.2. PD Homogeen.
Cirinya : M (x,y) dan N (x,y) homogeen dengan derajat yang sama.
Penyelesaiannya : substitusi y = ux ;
maka dy = u dx + x du
Selanjutnya PD bisa dipisah peubahnya.
1.3. M dan N adalah linear, tetapi tidak homogeen
Jadi PD yang berbentuk :
M dx + N dy = 0 menjadi (a1 x +b1 y +c1) dx + (a2 x +b2 y +c2 )dy = 0
Penyelesaian :
( i ) Apabila
![]() maka substitusi
maka substitusi

Selanjutnya PD menjadi :
P (x,t) dx + Q (x,t) dt = 0 yang dapat dipisah peubahnya
( ii) Apabila

maka selesaikan dulu sistem persamaan :
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
didapat akar : x = h dan y = k.
Kemudian substitusi :
x = u + h, maka dx = du
y = v + k, maka dy = dv
Selanjutnya PD menjadi PD Homogeen
1.4. M berbentuk y f (xy) dan N berbentuk x g (xy)
PD : M dx + N dy = 0 menjadi y f (xy) dx + x g (xy) dy = 0
Dengan substitusi z = xy, maka

PD akan menjadi : P(x,z) + Q(x,z) = 0 ; yang bisa dipisah peubahnya
2. PD EKSAK dan reduksi ke bentuk tersebut.
2.1. PD Eksak : M dx + N dy = 0 dengan ciri :

PD bisa ditulis sebagai : d µ = M dx + N dy = 0, dengan
![]()
![]()
Kedua µ ini identik; selanjutnya bisa dicari k(x) atau k(y).
Kemudian didapat µ
Penyelesaian PD : µ = C
2.2. Dengan mengalikan faktor integrasi F
PD yang tidak eksak menjadi Eksak.
PD : M dx + N dy = 0 tidak eksak
dan PD : MF dx + FN dy =0 menjadi eksak.
(i) Apabila

maka : ![]()
(ii) Apabila

maka : 
2.3. Apabila

maka :

2.4. Apabila

maka

2.5. Apabila


Dan PD : F (M dx + N dy) = 0 menjadi Eksak.
3. PD LINEAR ORDE SATU dan Reduksi ke bentuk tersebut.
3.1. Bentuk PD Linear Orde Satu :


Mempunyai Penyelesaian :

3.2. PD Bernoulli
Bentuk dari PD Bernoulli :

Bentuk tersebut bisa diubsh menjsdi :

:: Selanjutnya dengan substitusi :  didapat :
didapat :

PD akan menjadi :

yang merupakan PD Linear Orde Satu
II. PD ORDE SATU DERAJAT TINGGI
2.1. PD Orde Satu Derajat Tinggi dengan bentuk;

(i) Apabila PD bisa menyelesaikan p,
PD bisa difaktorkan menjadi

berarti

Sehingga penyelesaian PD :

(ii) Apabila PD bisa menyelesaikan y, berarti

apabila diturunkan terhadap x didapat

didapat penyelesaian

Selanjutnya p dieliminasi dari

Atau : Nyatakan x dan y dalam parameter p
(iii) Apabila PD bisa menyelesaikan x, berarti

Bila diturunkan terhadap y didapat

didapat penyelesaian :

Selanjutnya p di eliminasi dari
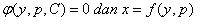
Atau : Nyatakan x dan y dalam parameter p
2.2. PD LAGRANGE
Bentuk PD Lagrange :

Turunkan PD Lagrange terhadap x

Penyelesaian PD ini

Didapat penyelesaiannya.
2.3. PD CLAIRAUT
Bentuk PD Clairaut

Penyelesaian PD ini dengan cara mengganti “p” pada PD Clairaut dengan “C”.
Sehingga penyelesaiannya :

III. PD LINEAR ORDE TINGGI dengan KOEFISIEN KONSTAN.
3.1. Bentuk umum PD Linear Orde Tinggi dengan koefisien konstan :
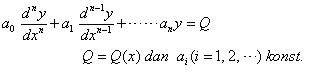
Operator D :

Beberapa sifat dan contoh penggunaan operator D :
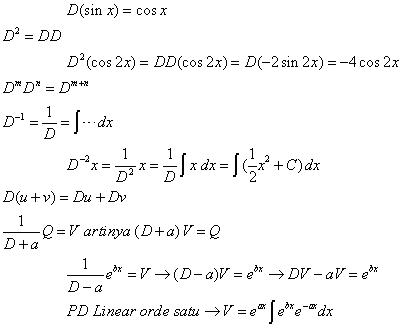
Jadi PD Linear Orde Tinggi dengan koefisien konstan, bila dinyatakan dalam operator D menjadi

3.2. PD Linear Homogeen dengan koefisien konstan
Bentuk :

Selanjutnya F (D) = 0 disebut Persamaan Karakteristik.

Beberapa kemungkinan bentuk dari akar karakteristik.
(i) :

(ii) :

dengan m = m1
(iii) : (iv) :
(iv) :
 Bentuk ke (iv) ini boleh ditulis dalam bentuk lain seperti berikut
Bentuk ke (iv) ini boleh ditulis dalam bentuk lain seperti berikut
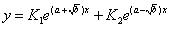 3.3. PD Linear Tidak Homogeen dengan koefisien konstan
Bentuk :
3.3. PD Linear Tidak Homogeen dengan koefisien konstan
Bentuk :
 Penyelesaian PD Linear Tidak Homogeen ini mempunyai dua buah penyelesaian, yaitu
Penyelesaian PD Linear Tidak Homogeen ini mempunyai dua buah penyelesaian, yaitu
 dan
dan  sehingga didapat Penyeleasaian PD Linear (Tidak Homogeen) :
sehingga didapat Penyeleasaian PD Linear (Tidak Homogeen) :
 Penyelesaian homogeen telah dibahas. Ada beberapa cara untuk mendapatkan Penyelesaian Partyikular.
1. Mereduksi orde.
(i). Merupakan penyelesaian berturutan dari PD Linear Orde Satu.
Penyelesaian homogeen telah dibahas. Ada beberapa cara untuk mendapatkan Penyelesaian Partyikular.
1. Mereduksi orde.
(i). Merupakan penyelesaian berturutan dari PD Linear Orde Satu.

 (ii). Dijadikan Pecahan parsial.
(ii). Dijadikan Pecahan parsial.
 2. Metode Variasi Parameter .
Untuk mencari penyelesaian partikular, dibentuk Fungsi L, yaitu dengan jalan mengganti C pada penyelesaian homogeen dengan L(beserta indeksnya) .
Adapun langkah-langkahnya sebagai berikut:
(i). Cari
2. Metode Variasi Parameter .
Untuk mencari penyelesaian partikular, dibentuk Fungsi L, yaitu dengan jalan mengganti C pada penyelesaian homogeen dengan L(beserta indeksnya) .
Adapun langkah-langkahnya sebagai berikut:
(i). Cari
 (2)
(2)
 (3)
(3)
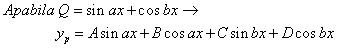 (4)
(4)
 (5)
(5)
 (6)
(6)
 (7)
Apabila suku dari Q sebut u , juga suku dari penyel. hom yang berasal dari akar karakteristik m yang kembar s . maka suku dari penyel. partikularnya menjadi x pangkat s kali u plus ……
(7)
Apabila suku dari Q sebut u , juga suku dari penyel. hom yang berasal dari akar karakteristik m yang kembar s . maka suku dari penyel. partikularnya menjadi x pangkat s kali u plus ……
 (8)
Apabila suku dari Q adalah x pangkat r kali u (u adalah suku dari penyel. hom yang berasal dari akar karakteristik m yang kembar s , maka suku dari penyel. partikular menjadi x pangkat (r + s) kali u plus ……
(8)
Apabila suku dari Q adalah x pangkat r kali u (u adalah suku dari penyel. hom yang berasal dari akar karakteristik m yang kembar s , maka suku dari penyel. partikular menjadi x pangkat (r + s) kali u plus ……
 4. Metode Singkat.
Untuk bentuk-bentuk khusus dari Q bisa penyel. partikular
4. Metode Singkat.
Untuk bentuk-bentuk khusus dari Q bisa penyel. partikular
 dengan metode yang singkat.
(1).
dengan metode yang singkat.
(1).
 (2).
(2).
 (3).
(3).
 (4).
(4).
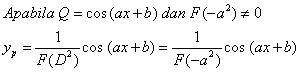 (5).
(5).
 (6).
(6).
 (7).
(7).

 Apabila Q = cos ax atau Q = sin ax , penyelesaiannya adalah
berturut-turut Bagian Real atau Bagian Imaginair dari :
Apabila Q = cos ax atau Q = sin ax , penyelesaiannya adalah
berturut-turut Bagian Real atau Bagian Imaginair dari :
 (8). Apabila Q adalah polinomial, atau
(8). Apabila Q adalah polinomial, atau
 (9).
(9).
 (10).
(10).
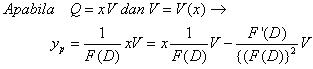 IV. PD LINEAR DENGAN KOEFISIEN VARIABEL.
( PD Cauchy dan PD Legendre)
4.1. PD CAUCHY
Bentuk :
IV. PD LINEAR DENGAN KOEFISIEN VARIABEL.
( PD Cauchy dan PD Legendre)
4.1. PD CAUCHY
Bentuk :
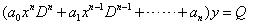 Penyelesaian : dengan substitusi
Penyelesaian : dengan substitusi

 maka PD akan menjadi :
maka PD akan menjadi :
 4.2. PD LEGENDRE
Bentuk :
4.2. PD LEGENDRE
Bentuk :

 PD akan menjadi :
PD akan menjadi :


Sdr. Tamurin yang baik,
Sebetulnya sudah saya coba untuk menyelesaikannya. Tetapi ada kendala dalam mengintegralkan. Pengin tahu dimana letak kegagalan dalam penyelesaian? Saya tunggu respon anda.
Paulhars.
By: paulusharsono on November 3, 2009
at 3:13 am